Courbes et surfaces de Bezier

    OpenGl integre un certain nombre de courbes et de surfaces, dont celles de Bezier. Pour les calculer, deux fonctions interviennent :
        - glMap : entre les parametres d'une courbe / surface (les points de controle d'une courbe de Bezier par exemple)
        - glEvalCoord : evalue un point de la courbe / surface

    Directement tire de l'exemple "bezcurve" du redbook, changer dans OnPaint :

    glPushMatrix();
        gluLookAt(0, 0, 0,
                  0, 0, -1,
                  0, 1, 0);
        static GLfloat ctrlpoints[4][3] = {
            {-4.0, -4.0, -15.0}, {-2.0, 4.0, -15.0},
            { 2.0, -4.0, -15.0}, { 4.0, 4.0, -15.0}};
        glColor3f(1.0f,1.0f,1.0f);
        glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
        glEnable(GL_MAP1_VERTEX_3);
        glBegin(GL_LINE_STRIP);
        for (GLfloat i = 0.0; i <= 1.0; i+=0.05f)
            glEvalCoord1f(i);
        glEnd();
        glDisable(GL_MAP1_VERTEX_3);

        glPointSize(5.0);
        glColor3f(1.0, 1.0, 0.0);
        glBegin(GL_POINTS);
        for (int j = 0; j < 4; j++)
            glVertex3fv(&ctrlpoints[j][0]);
        glEnd();
    glPopMatrix();

    glFlush();

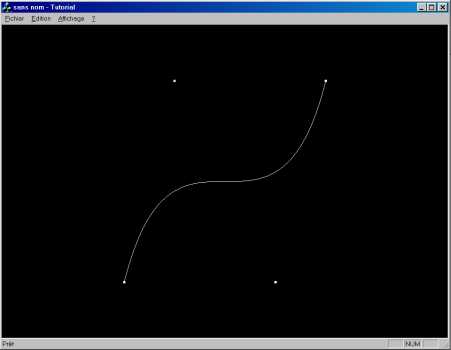
    Ce qui affiche une courbe de Bezier partant de (-4,-4) et allant en (4,4).

    Les parametres de glMap :
        - "1f" : indique une courbe (dimension 1) parametree par des float
        - GL_MAP1_VERTEX_3 : c'est un cacul qui concerne des points (vertex), ayant 3 coordonnees
        - la courbe commence a un index 0.0 et fini en 1.0 (voir glEvalCoord)
        - 3 : nombre de float ou double entre chaque groupe de coordonnees (ne sert que si les points sont dans un tableau de struct ou autre)
        - 4 : nombre de points de controle
        - adresse du debut du tableau de points de controle

    Ensuite pour lancer l'evaluation de la courbe, utiliser glEvalCoord1f avec comme parametre un index de la courbe (ici compris entre 0.0 et 1.0). Il est possible d'indiquer des valeurs en dehors de la plage, cela prolonge la courbe.

    Ce qui est genant, c'est que je n'ai aucune idee de l'utilisation qu'on peut en faire.

    Il est possible de faire la meme chose avec des couleurs, avec pourqouoi pas un peu d'animation :

        static GLfloat ctrlpoints[4][3] = {
                {-4.0, -4.0, -15.0}, {-2.0, 4.0, -15.0},
                { 2.0, -4.0, -15.0}, { 4.0, 4.0, -15.0}};
        static GLfloat ctrlpoints2[4][4] = {
                { 1.0, 0.0, 0.0, 1.0}, { 0.0, 1.0, 0.0,1.0},
                { 0.0, 0.0, 1.0, 1.0}, { 1.0, 1.0, 1.0,1.0}};
        ctrlpoints2[0][0] = float(0.5 + sin(tt/500)/2);
        glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
        glMap1f(GL_MAP1_COLOR_4, 0.0, 1.0, 4, 4, &ctrlpoints2[0][0]);
        glEnable(GL_MAP1_VERTEX_3);
        glEnable(GL_MAP1_COLOR_4);
        glBegin(GL_LINE_STRIP);
        for (GLfloat i = 0.0; i <= 1; i+=0.01f)
            glEvalCoord1f(i);
        glEnd();
        glDisable(GL_MAP1_VERTEX_3);
        glDisable(GL_MAP1_COLOR_4);
        glPointSize(5.0);
        glColor3f(1.0, 1.0, 0.0);
        glBegin(GL_POINTS);
        for (int j = 0; j < 4; j++)
            glVertex3fv(&ctrlpoints[j][0]);
        glEnd();

   

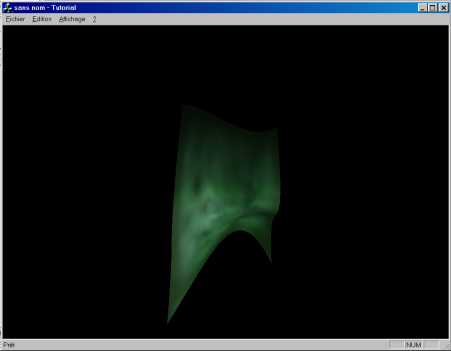
    Pour les surfaces, c'est exactement la meme chose, avec un "2" au lieu d'un "1" dans le nom des fonctions. Pour changer, directement tire de l'exemple "bezsurf" du redbook :

        static GLfloat ctrlpoints[4][4][3] = {
            {{-1.5, -1.5,   4.0-15.0}, {-0.5, -1.5,  2.0-15.0},
             { 0.5, -1.5, -1.0-15.0}, { 1.5, -1.5,  2.0-15.0}},
            {{-1.5, -0.5,   1.0-15.0}, {-0.5, -0.5,  3.0-15.0},
             { 0.5, -0.5,   0.0-15.0}, { 1.5, -0.5, -1.0-15.0}},
            {{-1.5,  0.5,   4.0-15.0}, {-0.5,  0.5,  0.0-15.0},
             { 0.5,  0.5,   3.0-15.0}, { 1.5,  0.5,  4.0-15.0}},
            {{-1.5,  1.5, -2.0-15.0}, {-0.5,  1.5, -2.0-15.0},
             { 0.5,  1.5,   0.0-15.0}, { 1.5,  1.5, -1.0-15.0}}
        };
        glEnable(GL_LINE_SMOOTH);
        glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4, 0, 1, 12, 4, &ctrlpoints[0][0][0]);
        glEnable(GL_MAP2_VERTEX_3);
        glRotatef(float(180.0*sin(tt/1000)), 0.0, 0.0, 1.0);
        glColor3f(1.0, 1.0, 1.0);
        for (int j = 0; j <= 8; j++)
        {
            glBegin(GL_LINE_STRIP);
            for (int i = 0; i <= 30; i++)
                glEvalCoord2f((GLfloat)i/30.0f, (GLfloat)j/8.0f);
            glEnd();
            glBegin(GL_LINE_STRIP);
            for (i = 0; i <= 30; i++)
                glEvalCoord2f((GLfloat)j/8.0f, (GLfloat)i/30.0f);
            glEnd();
        }
        glDisable(GL_MAP2_VERTEX_3);

    Pour eviter d'avoir a ecrire une double boucle de for, la meme chose peut s'ecrire :

        glColor3f(1.0, 1.0, 1.0);
        glMapGrid2f(9, 0.0, 1.0, 9, 0.0, 1.0);
        glEvalMesh2(GL_LINE, 0, 9, 0, 9);
        glDisable(GL_MAP2_VERTEX_3);

    glMapGrid indique qu'il faut dessiner la plage [0.0, 1.0] (correspondant a celle de glMap), en la decoupant en 9 x 9. glEvalMesh dessine la grille, suivant le mode indique : GL_POINT, GL_LINE, GL_FILL. Ce dernier est le plus interessant, il dessine une surface pleine. En mettant un peu de lumiere, on obtient de tres bons resultats.

    De nouveau un peu de lumiere dans OnSize :

    glEnable(GL_LIGHTING);

    GLfloat lightZeroPosition[] = {5.0f, 0.0f, -10.0f, 1.0f};
    GLfloat lightZeroColor[] = {0.8f, 1.0f, 0.8f, 1.0f};

    glLightfv(GL_LIGHT0, GL_POSITION, lightZeroPosition);
    glLightfv(GL_LIGHT0, GL_DIFFUSE, lightZeroColor);
    glLightfv(GL_LIGHT0, GL_SPECULAR, lightZeroColor);
    glLightf(GL_LIGHT0, GL_LINEAR_ATTENUATION, 0.05f);
    glEnable(GL_LIGHT0);

    GLfloat white[] = {1.0f, 1.0f, 1.0f, 1.0f};

    glMaterialfv(GL_FRONT, GL_DIFFUSE, white);
    glMaterialfv(GL_FRONT, GL_SPECULAR, white);
    glMaterialf(GL_FRONT, GL_SHININESS, 20.0f);

    Et peu de changements dans OnPaint :

    glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4, 0, 1, 12, 4, &ctrlpoints[0][0][0]);
    glEnable(GL_MAP2_VERTEX_3);
    glEnable(GL_AUTO_NORMAL);

    glRotatef(float(180.0*sin(tt/1000)), 0.0, 0.0, 1.0);
    glColor3f(1.0, 1.0, 1.0);
    glMapGrid2f(50, 0.0, 1.0, 50, 0.0, 1.0);
    glEvalMesh2(GL_FILL, 0, 50, 0, 50);
    glDisable(GL_MAP2_VERTEX_3);

    Des qu'il y a de la lumiere, il faut des "normales" pour que l'eclairage soit correct. GL_AUTO_NORMAL, qui ne marche qu'avec glEvalMesh, indique qu'il faut calculer les normales en meme temps que les points.

    Alors que je ne savais pas trop quoi faire des courbes de Bezier, les surfaces, simples a parametrer et decoupables a volonte, sont tres utiles. Par exemple pour dessiner un sol vallonne. Ou faire une veille avec un cube, qui devient une sphere, une etoile... Ah ? Ca existe deja ?

    Mais un sol c'est quand meme mieux avec une texture :

    static GLfloat ctrlpoints[4][4][3] = {
        {{-1.5, -1.5,  4.0-15.0}, {-0.5, -1.5,   2.0-15.0},
         { 0.5, -1.5, -1.0-15.0}, { 1.5, -1.5,   2.0-15.0}},
        {{-1.5, -0.5,  1.0-15.0}, {-0.5, -0.5,   3.0-15.0},
         { 0.5, -0.5,  0.0-15.0}, { 1.5, -0.5, -1.0-15.0}},
        {{-1.5,  0.5,  4.0-15.0}, {-0.5,   0.5,  0.0-15.0},
         { 0.5,  0.5,  3.0-15.0}, { 1.5,   0.5,  4.0-15.0}},
        {{-1.5,  1.5, -2.0-15.0}, {-0.5,   1.5, -2.0-15.0},
         { 0.5,  1.5,  0.0-15.0}, { 1.5,   1.5, -1.0-15.0}}
    };
    static GLfloat texpts[2][2][2] = {{{0.0, 0.0}, {0.0, 1.0}}, {{1.0, 0.0}, {1.0, 1.0}}};

    static CTexture texture;
    static GLuint texture_num;

    if (!texture.GetData())
    {
        texture.ReadFile("Marbre.bmp");
        texture.BGRtoRGB();
        glGenTextures(1, &texture_num);
        glBindTexture(GL_TEXTURE_2D, texture_num);
        gluBuild2DMipmaps(GL_TEXTURE_2D, 3, texture.GetWidth(), texture.GetHeight(), GL_RGB, GL_UNSIGNED_BYTE, texture.GetData());
        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
        glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
        glEnable(GL_TEXTURE_2D);
    }
    glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4, 0, 1, 12, 4, &ctrlpoints[0][0][0]);
    glMap2f(GL_MAP2_TEXTURE_COORD_2, 0, 1, 2, 2, 0, 1, 4, 2, &texpts[0][0][0]);

    glEnable(GL_MAP2_VERTEX_3);
    glEnable(GL_MAP2_TEXTURE_COORD_2);
    glEnable(GL_AUTO_NORMAL);

    glRotatef(float(180.0*sin(tt/1000)), 0.0, 0.0, 1.0);
    glColor3f(1.0, 1.0, 1.0);

    glMapGrid2f(50, 0.0, 1.0, 50, 0.0, 1.0);
    glEvalMesh2(GL_FILL, 0, 50, 0, 50);
    glDisable(GL_MAP2_VERTEX_3);
    glDisable(GL_MAP2_TEXTURE_COORD_2);

    Rien de bien nouveau, mais l'effet est splendide. Parfois, en pensant au nombre de calculs que cela represente, je me dis que ceux qui ont concu OpenGL et les cartes 3D doivent bien se casser la tete.

    Code source : Tutorial9.zip

    Etape precedente     Etape suivante